What is a “small” set - measure theoretic and topological approach

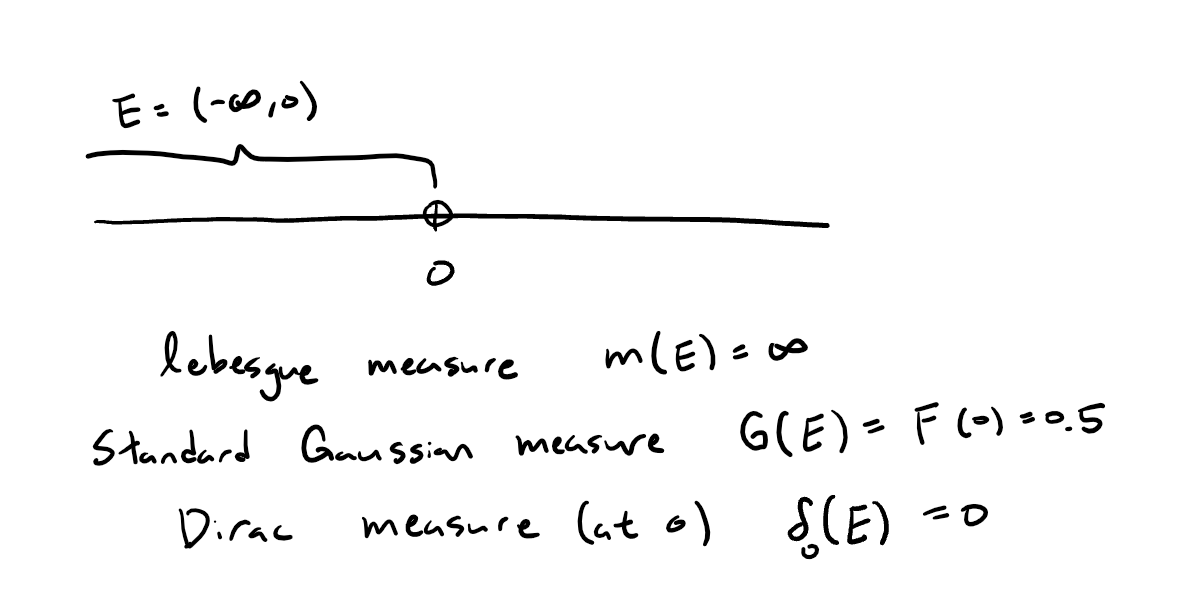
The notion of “smallness” in measure theory is pretty clear - when the set has measure $0$, then we can treat is as a small set, or a set with no mass. This is intuitive if we use a Lebesgue measure, but for other measures or distributions, this is not always the case. Take the Gaussian distribution for instance. The standard Gaussian distribution has almost no mass in $[c, \infty)$ for some sufficiently large $c$. However, if we use Lebesgue measure, it has infinite mass. So the idea of “smallness” is dependent on the measure we are using. A more dramatic example is the dirac delta measure. It has a point mass at 0 and the rest has measure 0. Is there a more general way to define “smallness” without dependence on any specific measure?

Notion of smallness depends on the measure we are using!

I introduce you Baire Category theorem - a topological way to define the notion of “smallness” of a set:

A set $E \subset X$ is of the first category in $X$ if $E$ is a countable union of nowhere dense sets in $X$. A set of the first category is sometimes said to be “meager.” A set $E$ that is not of the first category in $X$ is referred to as being of the second category in $X$.

A set $E \subset X$ is defined to be generic if its complement is of the first category.

Even though both measure function and Baire category theorem define the notion of smallness of a set, they do not imply each other. In fact, there is no link between the two. As Stein and Shakarchi says in their functional analysis book:

In general relying on one’s intuition about the category of sets requires a little caution. For instance, there is no link between this notion and that of Lebesgue measure. Indeed, there are sets in $[0, 1]$ of the first category that are of full measure, and hence uncountable and dense. By the same token, there are generic sets of measure zero.

Here’s a nice illustration from one of my favorite math blogs:

From Tai-Danae Bradley’s Math3ma blog (https://www.math3ma.com/)

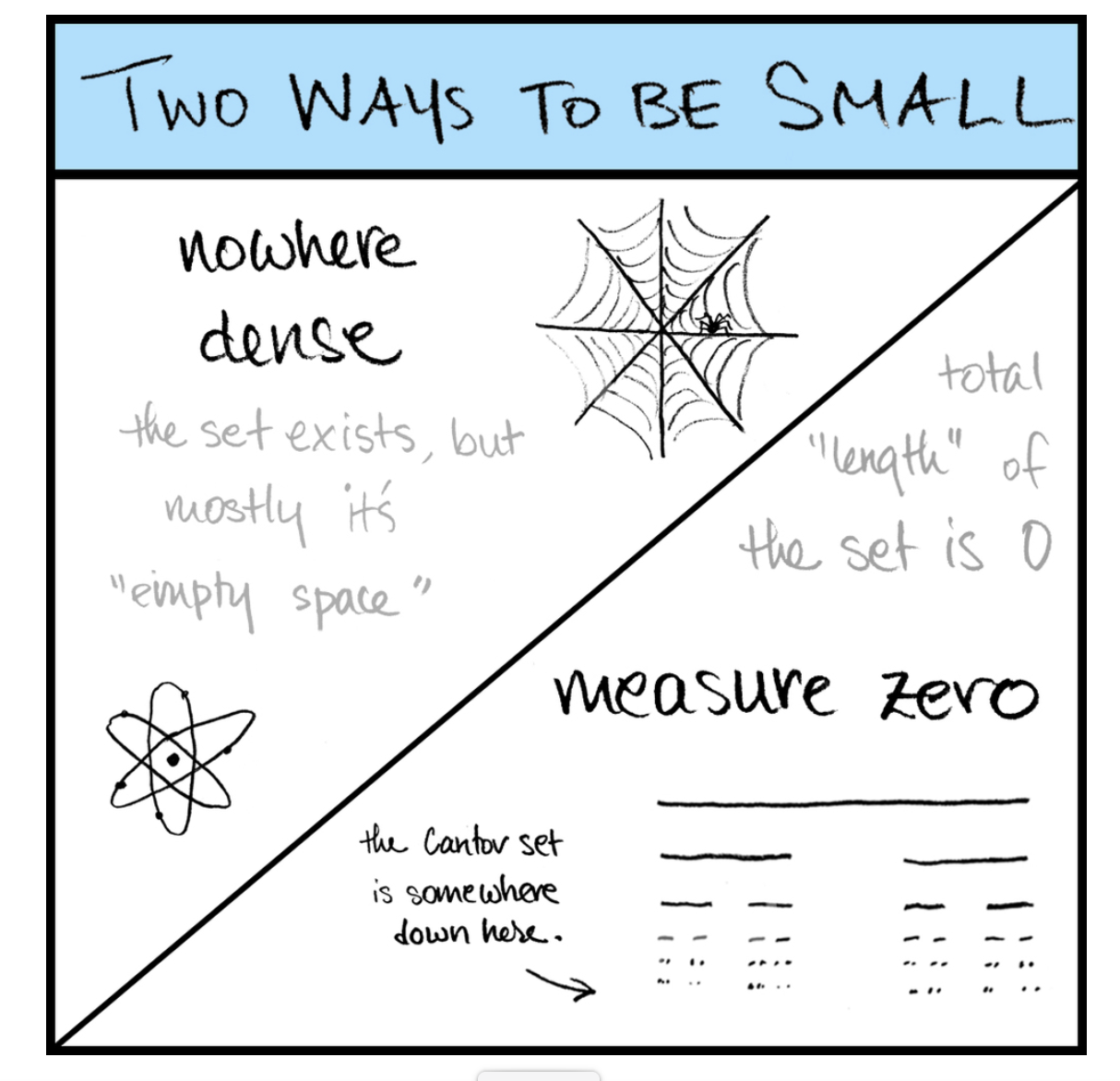
A fat cantor set is an example of a nowhere dense set (i.e. first category) that has a positive measure.